ผู้แต่ง: ผู้แก้ไขไซต์ ที่มา: เว็บไซต์
เมื่อเปรียบเทียบกับเลนส์สายตารูปทรงอื่นๆ เลนส์พระจันทร์โค้งมักไม่ค่อยถูกนำเสนอเป็นผลิตภัณฑ์สำเร็จรูป เลนส์ Moon Bending ส่วนใหญ่จะใช้ในการโฟกัสจุดเล็กๆ หรือการปรับแนวเลนส์ ในขณะที่เลนส์พลาโนนูนมักจะมีอัตราส่วนราคา/ประสิทธิภาพที่เหนือกว่า อย่างไรก็ตาม มีบางกรณีที่เลนส์ Bent-Moon ให้ประสิทธิภาพที่เหนือกว่าอย่างเห็นได้ชัดในราคาที่สูงกว่าเล็กน้อย
ความคลาดทรงกลม
เนื่องจากธรรมชาติของเลนส์เป็นทรงกลม ความคลาดเคลื่อนทรงกลมจึงสร้างรังสีขนานจากแกนแสงที่ระยะห่างต่างกันโดยไม่ตัดกันที่จุดเดียวกัน (รูปที่ 1) แม้ว่าเลนส์หลายตัวสามารถใช้เพื่อแก้ไขความคลาดเคลื่อนทรงกลมได้ แต่สำหรับระบบอินฟราเรดหลายระบบที่ต้นทุนวัสดุสูงกว่าวัสดุที่มองเห็นได้มาก แนะนำให้ลดจำนวนเลนส์ให้เหลือน้อยที่สุด แทนที่จะใช้เลนส์หลายตัว ความคลาดเคลื่อนทรงกลมของเลนส์ตัวเดียวสามารถลดลงได้โดยการปรับรูปร่างเลนส์ให้ได้รูปทรงที่เหมาะสมที่สุด
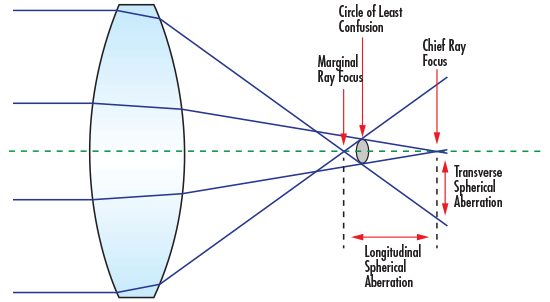
รูปที่ 1: ความคลาดเคลื่อนทรงกลม
สำหรับดัชนีการหักเหของแสงคงที่และความหนาของเลนส์ จะมีรัศมีรวมกันเป็นจำนวนอนันต์ ซึ่งสามารถนำมาใช้สร้างเลนส์ที่มีความยาวโฟกัสเฉพาะได้ การรวมกันของรัศมีเหล่านี้ทำให้เกิดรูปร่างเลนส์ที่แตกต่างกัน ซึ่งส่งผลโดยตรงต่อความคลาดทรงกลมและอาการโคม่าเนื่องจากความโค้งของแสงขณะผ่านเลนส์
รูปร่างของเลนส์สามารถอธิบายได้ด้วยปัจจัยรูปร่าง Coddington C (สมการที่ 1 และรูปที่ 2)

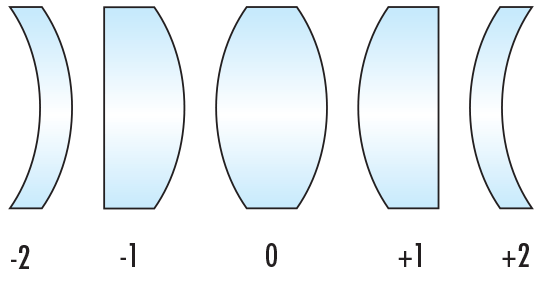
รูปที่ 2: ปัจจัยรูปร่างของ Coddington สำหรับการกำหนดค่าเลนส์ต่างๆ
ด้วยการใช้สมการความคลาดเคลื่อนของเลนส์แบบบาง (โดยใช้วัตถุที่ระยะอนันต์และตำแหน่งหยุดเลนส์) เราจึงสามารถหาสภาวะที่ทำให้เกิดความคลาดเคลื่อนทรงกลมขั้นต่ำได้ (สมการที่ 2)
สมมติว่าสามารถรักษาความยาวคลื่นให้คงที่ได้ สามารถมองเห็นความสัมพันธ์ระหว่างเลขชี้กำลังและปัจจัยรูปร่างที่ทำให้เกิดความคลาดเคลื่อนทรงกลมขั้นต่ำได้ (รูปที่ 3)

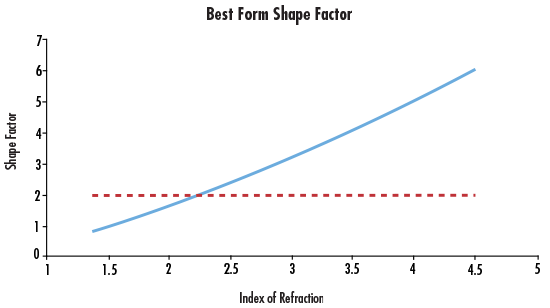
รูปที่ 3: ปัจจัยรูปร่างที่เหมาะสมที่สุดตามฟังก์ชันของดัชนีการหักเหของแสง
ข้อดีของการออกแบบพระจันทร์โค้ง
เมื่อทำงานในสภาพแวดล้อมที่มองเห็นได้ ดัชนีแก้วโดยทั่วไปจะอยู่ระหว่าง 1.5 ถึง 1.7 และรูปร่างของความคลาดเคลื่อนทรงกลมขั้นต่ำจะแทบจะนูนออกมา อย่างไรก็ตาม ในสภาพแวดล้อมอินฟราเรด มักใช้วัสดุดัชนีสูง เช่น เจอร์เมเนียม เจอร์เมเนียมที่มีสเปค 4.0 ให้ประโยชน์อย่างมากจากการออกแบบเลนส์พระจันทร์โค้งโดยการลดความคลาดเคลื่อนทรงกลมได้อย่างมาก
ความคลาดเคลื่อนทรงกลมน้อยที่สุดเกิดขึ้นเมื่อแสงโค้งงอสม่ำเสมอที่อินเทอร์เฟซทั้งสอง แม้ว่าพื้นผิวแรกของเลนส์เจอร์เมเนียมมูนจะทำให้แสงโค้งงอมากกว่าเลนส์ PCX ที่คล้ายกันเล็กน้อย แต่พื้นผิวที่สองของเลนส์ PCX จะทำให้แสงโค้งงอมากขึ้น ส่งผลให้ความคลาดเคลื่อนทรงกลมโดยรวมเพิ่มขึ้น
ดังแสดงในรูปที่ 4 ซึ่งเปรียบเทียบประสิทธิภาพของเลนส์เจอร์เมเนียม PCX ขนาด 25 x 25 มม. กับเลนส์เจอร์เมเนียมมูนเบนด์ขนาด 25 x 25 มม. ทำให้เห็นได้ง่ายว่าเลนส์ PCX หักเหแสงอย่างมีนัยสำคัญมากขึ้นอย่างไรเมื่อเทียบกับพื้นผิว ของเลนส์เมื่อเปรียบเทียบกับเลนส์โค้งพระจันทร์ ความโค้งที่เพิ่มขึ้นส่งผลให้ความคลาดเคลื่อนทรงกลมเพิ่มขึ้น เลนส์พระจันทร์โค้งเจอร์เมเนียมแสดงขนาดสปอตที่ลดลงอย่างมาก ทำให้เหมาะสำหรับการใช้งานอินฟราเรดที่มีความต้องการสูงมากขึ้น

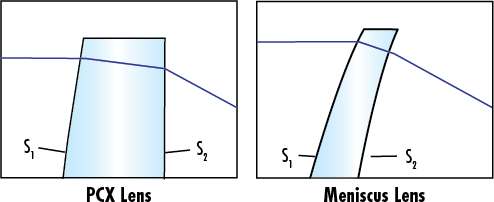
รูปที่ 4x: แผนภาพของเลนส์เจอร์เมเนียม PCX ขนาด 25 x 25 มม. เลนส์พระจันทร์โค้งเจอร์เมเนียม 25 x 25 มม.
| เลนส์นูนแบบแบน | เลนส์พระจันทร์โค้ง | |
| S1 ความคลาดเคลื่อนทรงกลม | 0.1 คลื่น | 2.4 คลื่น |
| S2 ความคลาดเคลื่อนทรงกลม | 14.2 คลื่น | 2.9 คลื่น |
| ความคลาดเคลื่อนทรงกลมทั้งหมด | 14.3 คลื่น | 5.3 คลื่น |
| ขนาดพิเศษ | 258μm | 83μm |
แม้ว่าเลนส์พระจันทร์โค้งจะยังคงให้ประสิทธิภาพที่สูงกว่าในส่วนที่มองเห็นได้ แต่เลนส์ที่ได้มักจะไม่เพียงพอที่จะชดเชยต้นทุนการผลิตที่เพิ่มขึ้น รูปที่ 1 แสดงการเปรียบเทียบประสิทธิภาพของเลนส์ PCX แคลเซียมฟลูออไรด์ (CaF25) ขนาด 50 x 2 มม. พร้อมเลนส์พระจันทร์โค้งในการใช้งานสเปกตรัมที่มองเห็นได้ และเลนส์ PCX เจอร์เมเนียม (Ge) 25 x 50 มม. พร้อมเลนส์พระจันทร์โค้งในการใช้งานอินฟราเรด . ขนาดเฉพาะจุดของเลนส์เจอร์เมเนียมจะลดลงอย่างมากเมื่อใช้รูปทรงพระจันทร์โค้ง
| ขนาดจุดเลนส์นูนธรรมดา | ขนาดจุดพระจันทร์โค้งงอ | ขนาดพิเศษ | ลดลงด้วยการดัดเลนส์พระจันทร์ |
| สเปกตรัมที่มองเห็นได้ (เลนส์ CaF2) | 849.3μm | 624.9μm | -26% |
| สเปกโทรสโกปีอินฟราเรด (เลนส์ Ge) | 258μm | 83μm | -68% |
ตารางที่ 1: การเปรียบเทียบขนาดจุดระหว่างเลนส์พลาโนนูนและเลนส์ดวงจันทร์โค้งสำหรับการใช้งานที่มองเห็นได้และอินฟราเรด
แม้ว่าเลนส์พระจันทร์โค้งอาจไม่ให้ประโยชน์ในการใช้งานทุกประเภท แต่ก็สามารถให้ข้อได้เปรียบด้านต้นทุนและประสิทธิภาพที่สำคัญสำหรับการใช้งานอินฟราเรดหลายประเภท รวมถึงสเปกโทรสโกปี
 ข่าวด่วน
ข่าวด่วน2023-06-06
2023-08-12
2023-08-19
2023-08-26